A continuation of my participation in the amazing Nand2Tetris course, by Noam Nisan and Shimon Schocken, now running on Coursera.
In this course you will build a modern computer system, from the ground up. We’ll take you from constructing elementary logic gates all the way through creating a fully functioning general purpose computer. In the process, you will learn how really computers work, and how they are designed.
If interested, see prior related post [DIY Computer Part 1 The NAND Gate]({% post_url 2016-03-06-diy-computer-nands %}).
Binary Addition
Half Adder
A half adder is a chip capable of summing two bits.
111
00010101
01011100
--------
01110001
^---1+1=2 (10 in binary, so write 0 and carry 1)
Lets boil down a single sum operation, so we can build it as a circuit.
From two input bits a and b, we need to determine two output bits, the sum, and the carry.
carry-->x
?????a??
?????b??
--------
x<--sum
This function can quite simply be represented as the following truth table, taking in two inputs, and producing two outputs:
| a | b | sum | carry |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Two prominant logic chips appear to meet the needs of the Half Adder.
Full Adder
In the case of the previous individual sum operation, we need to go a step further and be able to account for carry c, the carry calculated and propagated by the previous operation:
carry-->xc
?????a??
?????b??
--------
x<--sum
This is where a full adder plays an important role, being able to deal with three input bits a, b and c, and like the half adder produces two outputs sum and carry:
| a | b | c | sum | carry |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Multi-bit Adder
Now we have an individual step of the binary addition defined, thanks to the half and full adders, its just a matter of rinse and repeating by leveraging these chips.
A 16-bit Adder, a chip that takes two 16-bit buses and outputs a single 16-bit bus, therefore could be assembled using 15 Full Adders and a single Half Adder (for the rightmost bit which will never have a carry to worry about).
Negative Numbers
Signing bit
A scheme that involves sacrificing a single bit, used to represent positive and negative.
For example, in a three bit representation:
000 0
001 1
010 2
011 3
100 -0
101 -1
110 -2
111 -3
While it works, has some disturbing qualities, such as -0 (wtf), not only does this not make sense, it is wasteful of storage.
2’s Complement
A more elegant scheme that proposes to represent negative number -x using the positive number 2^n - x. For example, in a 3-bit representation, -3 is represented as 8 (2^3) minus 3 which is 5 or 101.
000 0
001 1
010 2
011 3
100 -4 (4)
101 -3 (5)
110 -2 (6)
111 -1 (7)
- positive number range
0...2^[n-1]-1 - negative number range
-1...-2[n-1]
Two’s complement has the totally elegant and free benefit of making it very easy to support negative numbers in the existing (Adder) circuits that have been designed.
For example:
-2 +
-3
In 2’s complement is really:
14 +
13
Which is:
1110 +
1101
-----
11011
^-----this carried over digit is truncated in binary addition
Without throwing away the carried over digit 11011 is decimal 27, but under binary addition is truncated to 1011 which is decimal 11, which in 2’s complement is -5 (16 - 11).
Negation
Given binary value x, determine -x (in 2s complement). On the surface a 2s complement binary negation function, conceptually appears straight forward. If it is indeed a low hanging fruit, we pickup the power of subtraction, without needing to design new chips/hardware. In other words:
y - x = y + (-x)
One proposal involves looking at the 2s complement concept from a slightly different angle:
2^n - x = 1 + (2^n - 1) - x
Huh, what does that even achieve? From a binary perspective has some attractive properties.
The value 1 or true is just a bus full of 1’s, for a 4-bit scheme is 1111, or 6-bits is 111111 and so on. To binary subtract a value from a bus full of 1’s, requires simply bit flipping, like this:
11111111 -
10101100
--------
01010011
A complete negation example. For an input of 4 (0100), would expect a result of -4 (1100 which is 12 in 2s complement).
1111 -
0100
----
1011 +
1
----
1100
The +1 operation is note worthy. A simple shortcut pattern is possible here, where you can flip the bits from right to left, stopping the first time 0 is flipped to 1.
Arithmetic Logic Unit (ALU)
The ALU is central in the notion of a Central Processing Unit, as originally proposed in the Von Neumann Architecture, and is responsible for computing a function f on two inputs, and outputting the result.
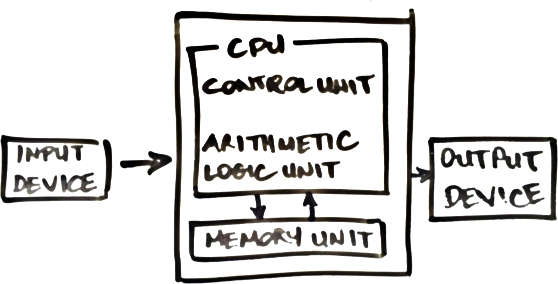
The function f is one from a pre-defined set:
- Arithmetic operations such as integer addition, subtraction, multiplication, division, and so on.
- Logical operations such as And, Or, Xor, and so on.
Carry look ahead. Adder optimisation for reducing the length of the carry daisy chain.